【半導体物性特論(材料)】第1回

【1】東京工業大学大学院 物質理工学院の授業の復習です。
【2】自身の勉強のためのものであり、間違いがある場合があります。
授業内容箇条書き
1. SiとGaAsのバンド図の違い (間接遷移と直接遷移)

図中の「伝導帯の底」と「価電子帯の頂上」に着目すると、
Si:価電子帯と伝導帯の間で電子が遷移する際、波数kが変わる→間接遷移
GaAs:電子が遷移する際、波数kがあまり変わらない。→直接遷移
それぞれの特徴を持つ半導体を間接遷移型半導体・直接遷移型半導体という。
間接接遷移型の半導体では、伝導帯の底と価電子帯の頂上が同じ波数ベクトルの位置に存在しないため、結晶運動量(h/2π)kのやり取りなしに電子・ホールは再結合することはができない。この場合、再結合エネルギーは格子振動として放出されることが多く、光は放出されないか、生じても非常に弱い発光となる。→太陽電池 (再結合速度が重要)
直接遷移型半導体では、伝導帯の下端にいる電子は、価電子帯の上端にいるホールと運動量のやり取りなしに再結合することができ、再結合のエネルギーは光として放出される。→発光ダイオードなどに活用
再結合のスピードも当然、直接遷移(~nsec位)より間接遷移(µsec~msec)の方が遅い。
2. キャリア濃度
半導体のキャリアには以下の二つが挙げられる。
2-1. キャリア濃度はどれくらいなのか?
例としてSi半導体を用いる。まずは計算問題。
Si半導体はダイヤモンド構造を有する。格子定数がa=5.43Åとすると、各辺1cmのサイコロサイズ中にいくつのSi原子が存在するか?

結果5.0×10^(22)個ものSi原子がサイコロ中に入っていることが分かった。他の原子についても密度の違いはあれど10^(22) 個/cm3というオーダーが成り立つ。
これを用いると金属原子から放出される自由電子もおおよそ10^(22) 個/cm3であることがわかる。これがキャリア濃度の上端になる。
また、Siの真性半導体(ドーピングなし)のキャリア密度はおよそni=10^(10) 個/cm3 (室温)とされる[*1]。これはキャリア濃度の下端レベルである。
ちなみに、Siのバンドギャップエネルギー(Eg)は1.12 eVであり、電子の平均エネルギーは26 meVである。そのエネルギー差は43倍であるが、真性半導体のキャリア濃度niからもわかるようにSiのEgを飛び越えることができる電子は10^(12)個に1個の割合で存在している。
従ってキャリア濃度は10^(10) 個/cm3~10^(22) 個/cm3の間になる。一般的に10^(15) 個/cm3~10^(18) 個/cm3位のキャリア濃度が使われるらしい。
3. オームの法則

ここで、図中下側の式を見ると、µEは単位が[cm/s]となり速度vとなる。
つまりv∝µ, v∝E。移動度は高いと電気伝導率が高くなるため、材料の物性でも重要となる。
東工大 物質理工学院 材料系 R3年度(2022大修) II-05 熱力学

【1】東京工業大学大学院 物質理工学院の過去問を自身の勉強のために解いたものです。
【2】必ずしも解答を保証するものではありせん。間違いがある場合があります。
【3】過去問は各自で手に入れてください。
オットーサイクルに関する設問
(1)状態Bにおける温度
TB=630 [K],, (6)解説に示す。
解説:
問題文より与えられた、断熱過程における関係式「TVR/Cv=一定」によって求める。求めたいのはTBであるので状態Aから状態Bの断熱過程について計算する。

(2)断熱圧縮過程の仕事
(2)ΔWAB=8.22 [kJ]
解説:
状態Aから状態Bへの変化は断熱過程(dQ=0)であるので、系に対する仕事をwinとして、熱力学第一の法則「dU=dQ+dwin」は「dU=dwin」と整理することができる。ΔWABはサイクル図から圧縮過程であり、系に対する仕事であるので、整理した熱力学第一の法則をそのまま使うことができる(符号的な意味で)。内部エネルギーの関係式「dU=nCvdT」を用いると以下のように計算できる。
※問題文よりn=1 [mol]
![]()
(3)定積変化におけるQin
Qin=27.1 [kJ]
解説:
状態Bから状態Cは定積変化であるので、非膨張仕事が存在しないとすると「dw=0」となる。従って、熱力学第一の法則は「dU=dQ」と整理できる。内部エネルギーの関係式「dU=nCvdT」を用いると以下のように計算できる。
※問題文よりn=1 [mol]
![]()
ここで、計算にはTCが必要となる。TCは(1)と同様、断熱過程に着目して計算する。

求めたTCを用いてQinは以下のように計算できる。
![]()
(4)断熱膨張過程における内部エネルギー変化
ΔUCD=-22.9 [kJ]
解説:
内部エネルギーの関係式「dU=nCvdT」を用いて以下のように計算できる。
![]()
(5)熱機関の熱効率
η=54.2 [%]
解説:
熱効率ηとは、「取り入れた熱を、どれだけ有効な仕事として使ったかの割合」を指す。以下にオットーサイクルのPV図と計算方法図を示す。

〇熱効率は「全ての仕事を足し合わせ、取り入れた熱で除すことで得られる」。仕事は外界に対する仕事の場合(正)、系に対する仕事の場合は(負)である。
〇各状態変化において熱の出入りと発生する仕事について考える。
・状態Aから状態B:断熱圧縮過程, dQ=0, dwin
・状態Bから状態C:定積過程, dQin, dw=0
・状態Cから状態D:断熱膨張過程, dQ=0, dwout
・状態Dから状態A:定積過程, dQout, dw=0
ここで、WCDが-ΔUCDとなるのは、(2)と同様、断熱過程であるため。断熱過程における熱力学第一の法則「dU=dwin」の関係より、外界への仕事は符号が変わって「dwout=-dU」である。
(6)熱サイクルの温度T, エントロピーS図

解説:
TS図は熱力学第二の法則「dS≧dQ/T」を用いて考える。
・断熱過程はdQ=0であるため、dS=0
・定積過程は吸熱(dQin)のときdS>0, 放熱(dQout)のときdS<0
従って、上図が完成する。
【回折結晶学】回折現象とエバルト球

【1】東京工業大学大学院 物質理工学院の授業の復習です。
【2】自身の勉強のためのものであり、間違いがある場合があります。
1. 回折現象とは
波が障害物の背後に回り込む現象のこと。波は一見すると到達できない領域に回り込む。これはホイヘンスの原理を認めることで以下のように理解することができる。
※ホイヘンスの原理:波は波面上の各点から球面波(素元波)を無数に発生し、それらに共通する面が次の瞬間の波面になると考える。

2. Braggの回折条件と逆格子ベクトルへの適応
Braggの式は結晶におけるX線回折を説明する式で、面間隔dを持つ平行な原子面群を考えたとき、隣り合う原子面の行路差が2dsinθとなることから、これがX線の波長の整数倍(n倍)と等しければ強い回折X線を生じるということを表す。

つまり、Braggの式は「2dsinθ=nλ」となる。
次に、実格子で捉えてきたこの式を逆格子ベクトルで記述することを考える。

上図はhkl面についてBraggの回折条件を示した図である。ここで、S0およびSはそれぞれ、入射ベクトルの単位ベクトル、反射(回折)ベクトルの単位ベクトルである(つまり大きさ|S0|=|S|=1ということ)。図のように二つの単位ベクトルの差を取ると、hkl面に垂直で大きさが2sinθとなるベクトルが得られる。この向きは逆格子ベクトルに等しい。また、dhklの逆数は逆格子ベクトルの長さとなる、これらをBraggの式に当てはめると式中に逆格子ベクトルを出現させることができる。
3. Ewald球 (エバルト球)
逆格子ベクトルで記述したBraggの式を絵に示したものが以下の図である。

エバルト球とは、ある逆格子点Oから、入射方向に沿って1/λだけ離れた点Aを中心とした半径1/λの円である。逆格子点が球(円)上にあるときは逆格子ベクトルが回折条件を満たすことになる。つまり、エバルト球は回折する逆格子点を視覚的に表すことができる。
しかし、工夫をせずに使うとエバルト球上にくる逆格子点はめったに存在しないため、回折がほとんど観測できない。実際の実験系ではエバルト球上に逆格子点がでくわすように以下のような工夫が行われいている。
・粉末法:粉末試料は勝手な方向を向いているため、X線の入射方向と結晶の方位を変えることができる。これによりエバルト球上に逆格子点が出くわす可能性が上がるため、回折を観測しやすくなる。
・ラウエ法:様々な波長を含む白色X線を用いることでエバルト球の半径(1/λ)を可変にできる。これによりエバルト球が幅を持つため、回折を観測しやすくなる。入射方向や結晶の方向は固定。
【無機表面化学】様々な表面と表面の緩和

【1】東京工業大学大学院 物質理工学院の授業の復習です。
【2】自身の勉強のためのものであり、間違いがある場合があります。
- 固体表面
- 1. 表面化学における表面の分類
- 2. 表面の緩和
- 2-1. 表面緩和 (surface relaxation)
- 2-2. 表面再構成 (surface reconstruction)
- 2-3. 表面欠陥 (surface defects)
固体表面
固体表面とは固相と気相(あるいは液相)の界面のことであり、バルク(固体内部)とは異なる組成や構造、物性を有することから非常に重要な部分である。
1. 表面化学における表面の分類
〇 理想表面 (ideal surface)
理想的な三次元結晶を切断して得られる、完全に規則的かつ平滑な二次元表面。理想の名の通り、表面化学を考察する上で用いられる仮想的な表面。
〇規定表面 (well defined surface)
超高真空技術などの実験的的手法によって、原子配列や化学組成などを再現性良く十分に制御された固体表面。
〇実表面 (real surface)
空気中に置かれた物質の表面で、種々の不純物が不規則に吸着している。原子配列なども乱れており、非晶質化していることもある。
2. 表面の緩和
表面では、そこで原子どうしの結合が途切れる結果、ダングリングボンド(原子の未結合手)を生じる。バルクとは異なり、一方の結合相手が存在しないため、表面の原子はバルクの原子と状態が異なっている。ダングリングボンドのエネルギーは高く、表面では以下のような現象が起きている。

2-1. 表面緩和 (surface relaxation)
二次元的な対称性(原子配列の二次元並進周期)は保ったまま、表面の原子間層距離を変化することによってエネルギーの緩和が起きる現象。
表面緩和の典型的なものは、表面に平行な原子面の間隔変化であり、金属では面内密度が低い層間距離の変化率が大きくなる傾向がある。
一般的に表面緩和は最上層の面間隔を小さくする方向に起き、表面からバルク内部へ振動するよう(下右図)に生じる。バルク内側に行くのは、原子が配位数を増やそうとするためであり、振動は層が進むにつれてバルクの値へと収束していく。

・ランプリング (rumpling)
最表面に2種類以上の原子が含まれており、単位胞内の各原子の緩和の大きさが異なる場合の表面緩和。

例としてNaClの100面の図を上に表示した。NaClの100面では陽イオンと陰イオンが交互に並んだ構造をしている。ここで、陽イオンはイオン半径が小さく分極率が小さいため、バルク内部に大きく変位する一方、陰イオンはイオン半径が大きく分極率が大きいため、バルク内部への引き付けが弱く、イオンの原子核よりも電子雲が引き込まれて安定化し、原子核の変位自体は小さくなる。
(もしくは陰イオン間で反発することで変位が小さくなるでもいい)
結果として、陽イオンと陰イオンではバルクへの変位に差が生じ、表面のイオンの位置はギザギザになる。
・バックリング (buckling)
構造緩和の電子的な起源がイオン結晶の場合はランプリングと呼ぶが、半導体の場合はバックリングという。構造はランプリングと同じようになる。GaAsのような化合物半導体で見られる。
2-2. 表面再構成 (surface reconstruction)
表面緩和と同様、エネルギー的に安定化するため、バルクの原子配列と異なる配置をとること。表面緩和とは異なり、表面再構成は表面の周期構造が変化する。
特に周期表下部の金属で起きやすく、種類や程度は温度に依存する。
再構成された表面はウッドの記法に基づいて記述されることが多い。
2-3. 表面欠陥 (surface defects)
固体表面で起きる、原子の空隙(vacancy)、気相からの原子の付加(adatom)、固体内の原子列欠損、ステップ(step, 1原子層から数原子層の段差)の形成、キンク(kink, ステップの折れ曲がりに相当する部分)などの欠陥や構造を総称して表面欠陥という。

参考文献
・中島章, 最新表面化学講座(第II講) 表面構造概論, 色材協会誌, Vol.85, No.9, p.389-394, (2012)
【回折結晶学】ステレオ投影図

【1】東京工業大学大学院 物質理工学院の授業の復習です。
【2】自身の勉強のためのものであり、間違いがある場合があります。
ステレオ投影図
1-1. ステレオ投影で対称性を示す方法(図の解釈不安)
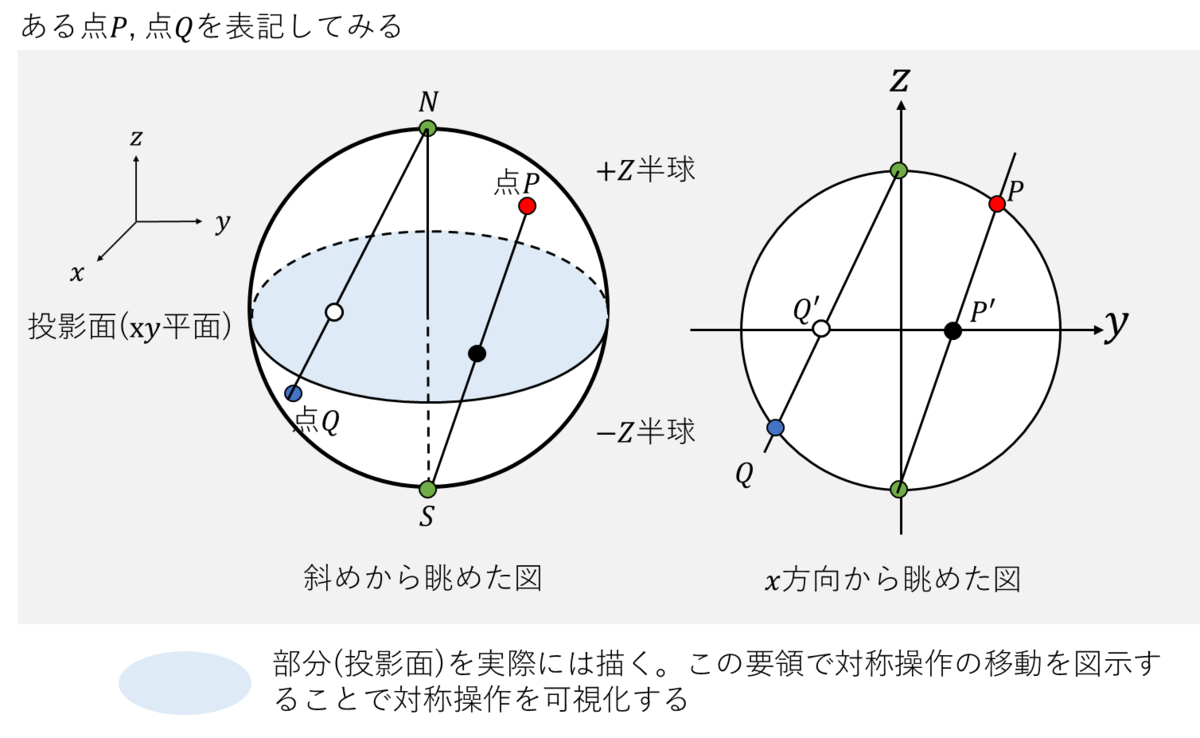
ステレオ投影図とは、結晶や分子に対称操作を施した結果を2次元に可視化できる。以下に約束事を示す。
・単位球の中心に結晶や分子を置く(図には描いていない)
・+Z半球内のある点(例:点P)と南極(S)を結ぶ直線がxy平面と交わる点をステレオ投影(例:点P')とする。
・-Z半球内のある点(例:点Q)の場合は北極(N)を用いる(例:点Q')。
・通常、+Z軸方向から観測し、+Z半球内の投影点であれば○、-Z半球内の投影点であれば●でxy平面に記述する。
参考文献
・Burns[著] 寺内ら[訳], 結晶としての固体, 東海大学出版会, (1998)
1-2. ステレオ投影で対称性を表す際に用いる記号
ステレオ投影で対称性を表す際に用いる主な記号を以下に示す(一部)。
※もっと知りたい場合は参考文献からURLを踏んでみてください。

参考文献
・Advanced Certificate in Powder Diffraction on the Web, Symmetry Symbols, Accessed:2022/06/28
1-3. 実際にステレオ投影を用いて対称性を表記してみる。
1-3-1. 水分子の対称性
H2O分子は以下に示すような対称性を有する。すなわち記号で表記するとE(1), C2(2), 2σv(m)の4つである。

位置1を出発位置とすると、E(1)では位置が変わらないため位置1のままとなる。位置1にC2(2)を行うと位置2に移動する。位置1にσv(m)を行うと位置3になる。また位置1にもう一方のσv(m)を行うと位置4になる。
1-3-2. E, C4, C2, C43,2C2', 2C2'', i, S4, S43, σh, 2σv, 2σd, を記述する(ちょっと不安)
位置1を出発点として、各操作を行った際のステレオ投影図を以下に示す。ここで、C2'の回転軸はσv面内、C2''の回転軸はσd面内にあるとする(ともにxy平面内にある)。

・E:位置1から何もしないため。位置1のまま。
・C4:位置1から主軸(4回回転軸)を基準に90度だけ反時計回りする。
・C2:位置1から主軸(4回回転軸)を基準に180度だけ反時計回りする。
・C43:位置1から主軸(4回回転軸)を基準に90度×3だけ反時計回りする。
・C2':位置1からσv面を通る回転軸を基準に180度だけ反時計回りする。σv面でxy平面を通るということは、主軸と垂直であるため、回転することで+Z半球の点(位置1)から-Z半球の点となる。
・C2'':位置1からσd面を通る回転軸を基準に180度だけ反時計回りする。σd面でxy平面を通るということは、主軸と垂直であるため、回転することで+Z半球の点(位置1)から-Z半球の点となる。
・i:位置1を反転させると、左右上下前後が反対になる。
・S4:位置1から主軸(4回回転軸)を基準に90度だけ反時計回りした後、σh面を鏡映面として対称移動させる。
・S43:位置1から主軸(4回回転軸)を基準に90度だけ反時計回りした後、σh面を鏡映面として対称移動させる。これを3回繰り返す。
・σh:σh面を鏡映面として対称移動させる。
・σv:σv面を鏡映面として対称移動させる。鏡映面は主軸を含む面であるから、主軸に垂直に対称移動するはず。そのため+Z半球から-Z半球への移動はないと思う。
・σd:σd面を鏡映面として対称移動させる。鏡映面は主軸を含む面であるから、主軸に垂直に対称移動するはず。そのため+Z半球から-Z半球への移動はないと思う。
※私が不安に感じているのはσvとC2'およびσdとC2''の位置関係です。多分あってると思いますが…。
【回折結晶学】対称操作 (点群)

【1】東京工業大学大学院 物質理工学院の授業の復習です。
【2】自身の勉強のためのものであり、間違いがある場合があります。
対称操作
結晶や分子における対称操作とは、操作を施した前後で見かけ上変化しないような操作のことを言う。そのため、対称操作を何度行おうとも、分子や結晶は等価な位置にあるままである。どのような操作が対称操作になるのか、結晶や分子で確認することでそれらの対称性を議論することができる。
1-1. 様々な対称操作
1-1-1. 対称操作の記号と操作の説明
記号は左側が「シェーンフリース記号」、右側が「ヘルマンモーガン記号」(国際表記)である。
 シェーンフリース記号と国際表記の対応はややこしいが、どちらもよく使われるので対応できるようにする必要がある。
シェーンフリース記号と国際表記の対応はややこしいが、どちらもよく使われるので対応できるようにする必要がある。
各操作を図で見てみよう(恒等操作は省く)

また、対称操作には対称要素がある。対称要素とは対称操作を行う足がかりになる点、直線、平面のことである。それぞれの対称操作に対応する対称要素を以下に示す。

1-1-2. シェーンフリース記号と国際表記の対応確認 (問題)
Q1:6 bar=S35であることを証明しなさい。
Q2:3 bar=S65であることを証明しなさい。
※国際表記で数字の上にbarを付ける方法が分からないので横にbarと記載。
※シェーンフリース記号の上付きの数字はその操作を行う回数を示している。
1-1-3. シェーンフリース記号と国際表記の対応確認 (解答)
Q1:6 barは「60度回転した後、反転中心を基準に反転」、S35は「120度回転した後、鏡映面を基準に対称移動。この操作を5回を行う」を表している。従って、以下のような操作になる。

Q2:3 barは「120度回転した後、反転中心を基準に反転」、S65は「60度回転した後、鏡映面を基準に対称移動。この操作を5回を行う」を表している。従って、以下のような操作になる。

従って、いずれにおいても同じ結果となった。
1-2. 対称操作の逆
分子や結晶に対してAの操作を行った後、つづいてBの操作を行った時、位置が完全に元に戻り、あたかも何の操作を行わなかったように見えたとする。この時、操作Bは操作Aの逆と言う。これらの関係を式に表すとBA=Eとなる。式に表す際は、約束として後に行う操作を先(左)に記述する。

上図に示すように、例(1)ではσ(m)のような対称操作はそれ自身の逆でもあることがわかり、例(2)ではC43(43)がC4(4)の逆であることが分かる。
参考文献
・Burns[著] 寺内ら[訳], 結晶としての固体, 東海大学出版会, (1998)
東工大 物質理工学院 材料系 H30年度(31大修) II-08 熱力学

【1】東京工業大学大学院 物質理工学院の過去問を自身の勉強のために解いたものです。
【2】必ずしも解答を保証するものではありせん。間違いがある場合があります。
【3】過去問は各自で手に入れてください。
カルノーサイクルに関する設問
(1)![]() , (2)
, (2)![]() , (3)
, (3)![]() ,
,
(4)![]() , (6)
, (6)![]()
(5)2通りの考え方を示す。

解説:
(1)等温過程(dT=0)において、温度の関数である内部エネルギー変化dUは0となるので、熱力学第一の法則「U=Q+Win」は「Q=Wout」のように式変形ができる。
![]()
※Winは系に対する仕事, Woutは外界に対する仕事である。
※pdVからの式変形は気体の状態方程式「PV=nRT」を用いている。
(2)断熱過程ではポアソンの式「PVκ=const.」が成り立つ。定数をAとすると断熱膨張過程における仕事は以下のように計算できる。

(3)※ポアソンの式の導出過程を以下に示す。

(3)(1)と基本的には同じ。圧縮過程は「系(の内部)に対して行う仕事」であることに注意する。
![]()
(4)(2)と基本的に同じ。断熱過程ではポアソンの式「PVκ=const.」が成り立つ。定数をAとすると断熱膨張過程における仕事は以下のように計算できる。ここで、圧縮仕事は「系に対する仕事」であることに注意する。

(5)解答と同じ
(6)熱効率(η)とは「外界から与えられた熱」でどれだけ「仕事」したかであるので、以下で与えられる。

上図のように断熱過程、等温過程におけるPVの関係を用いて等温膨張・圧縮仕事が符号以外等しいことを示す。